高校の教科書を見ていると、紙が足りないのか、随分と説明を省いた形で、難解な事柄が取り上げられている事が少なくない。 その一つが、「微分可能」と言うワードではないだろうか。教科書にはこうある。

「関数 \( f(x) \) について、極限値 \( \lim_{h \to 0} \frac{f(a+h)-f(a)}{h} \) が存在するとき、\( f(x) \) は \( x=a \) で微分可能である」

これを見て、こう思ったのではないだろうか。

極限値が存在する、とは?

先の単元で \( f(x)=x \) の極限は例えば \( \lim_{x \to \infty} \) において無限大に発散する事は習った。しかし、これは極限であり、極限値とは呼べない。 つまり、極限と極限値は似て非なるものであるという事だ。 極限値とは例えば0の様な値に収束する関数の収束先の値の事だ。要するに

極限→∞に発散したり、0などに収束することもある
極限値→例えば、0などに収束した際の0!


では、どの様な際に極限値が存在すると言えるのだろうか。 まず日本語で言うならば、右極限と左極限が一致するということだ。右極限、左極限とは例えば\( f(x)=x^2 \) というグラフにおいて、 \( x=0 \) に右から近づけますか？左から近づけますか？と言う話だ。

右極限(数式で書くと\( \lim_{h \to +0} x^2\))であれば、 \( x=0 \) に大きい方から近づけていった値、逆に小さい方から \( x=0 \) に近づけていった値を左極限(\( \lim_{h \to -0} x^2\))と言う。この２つは両方とも0に収束する。つまり、極限値は0となる。
これを先の \( \lim_{h \to 0} \frac{f(a+h)-f(x)}{h} \) について適応しようとすると大変だ。そこで式ではなく、グラフを使って考えてみたい。

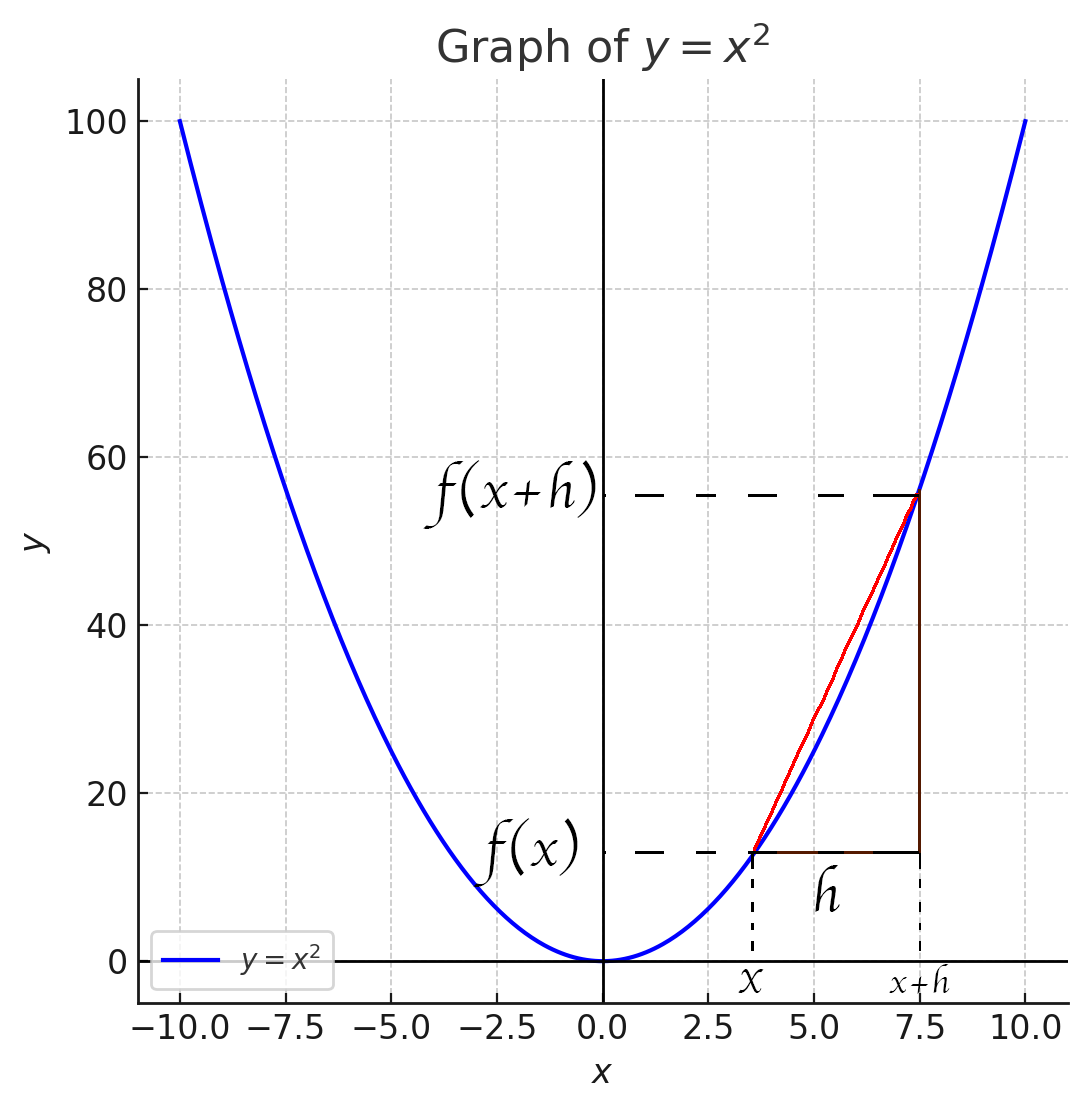
微分の定義について、少し書かせて頂く。例えば \( y=x^2 \) のグラフについて \( x \) という値の右側に \( x=x+h \) なる値を取り、 それを右側から近づけることで \( x \) における微分係数を求める。これが微分の定義で、上の図の赤線の傾きが正に\( \lim_{h \to 0} \frac{f(a+h)-f(a)}{h} \) となるわけだが、 微分を知っていた人は \( h \) と言えば、正の小さい値をイメージした人が多いのではないか。しかし、極限値を取る、と言う意味では \( h \) は負のパターンも考えねばならない。 そこで、\( \lim_{h \to +0} \frac{f(a+h)-f(a)}{h} \) と \( \lim_{h \to -0} \frac{f(a+h)-f(a)}{h} \) について考え、 これらが一致する際、「関数 \( f(x) \) について、極限値 \( \lim_{h \to 0} \frac{f(a+h)-f(a)}{h} \) が存在する」と言え、「\( f(x) \) は \( x=a \) で微分可能である」と言える。
少し話はズレるが、\( f(x) \) は \( x=a \) における極限値が存在するからと言って、\( x=a \) において連続であるとは限らない。反例として以下の様な滅茶苦茶な関数を紹介する。\( f(x) = \begin{cases} x^2 & (x \neq 0) \\ 1 & (x = 0) \end{cases} \)

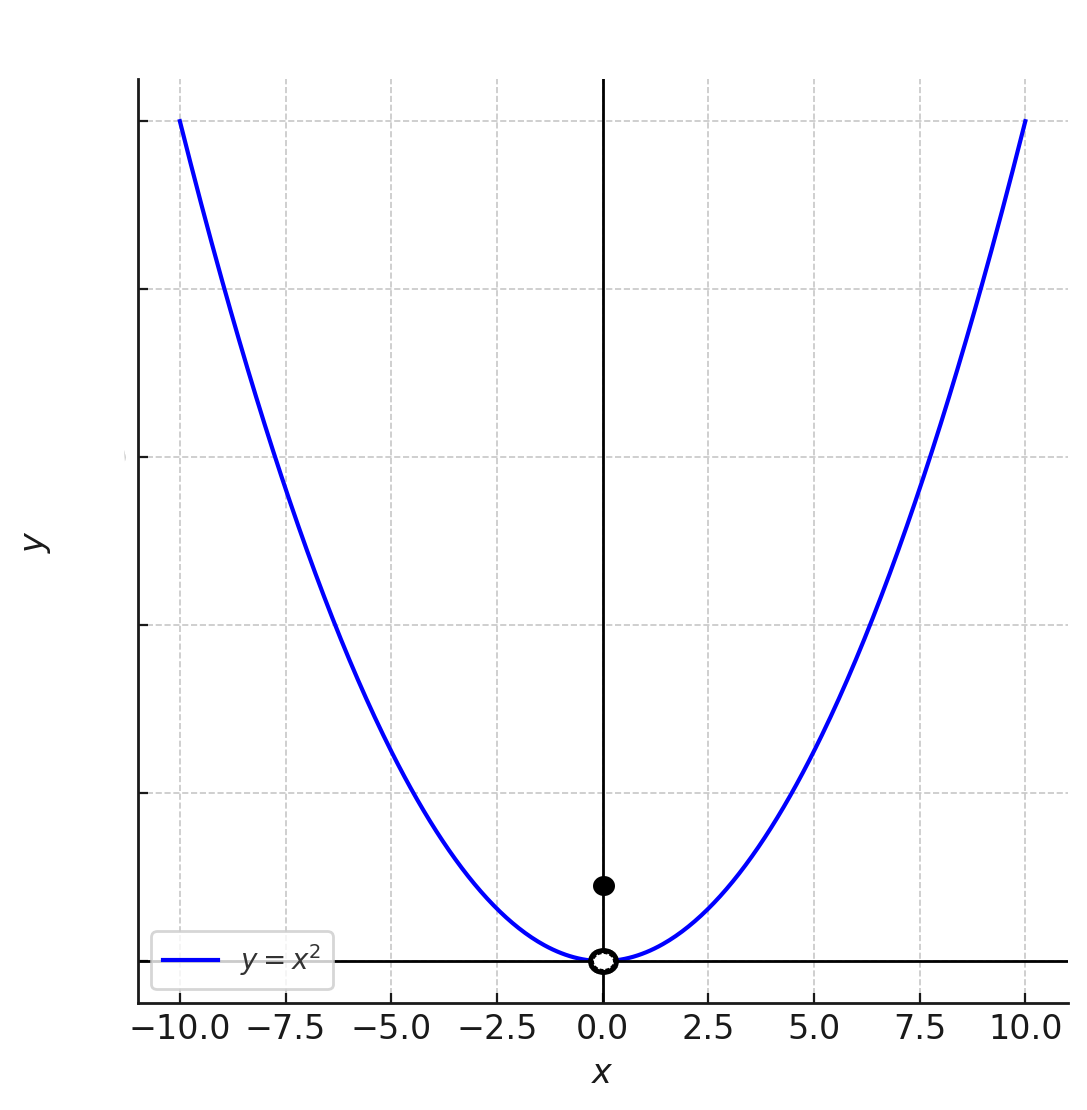
この関数において、\( x=0 \) における極限値は0と言える。 しかし、\( x=0 \) の際、\( f(0)=1 \) をとる。これは明らかに不連続である。要するに

x=aにおいて極限値が存在するからと言って、
x=aにおいて連続とは限らない


しかし、「関数 \( f(x) \) について \( f(x) \) は \( x=a \) で微分可能である」とき「関数 \( f(x) \) は \( x=a \) において連続である」は成立する。この証明については、どの教科書にも書いてあるので、是非そちらを見て頂きたい。 また、ついでに先ほどの \( f(x) = \begin{cases} x^2 & (x \neq 0) \\ 1 & (x = 0) \end{cases} \) と言う関数について微分可能なので連続になってしまうのではないか、と思った方については、「関数 \( f(x) \) について、極限値 \( \lim_{h \to 0} \frac{f(a+h)-f(a)}{h} \) が存在するかどうか、つまり微分可能かどうかをしっかり調べてみてほしい。