生徒から、確率の分野でPとCの違いが分からない、と聞かれます。 教科書的に言えば、PとはPermutation(順列)、CとはCombination(組み合わせ)なのですが、そんなこと言われても、よくわかりませんよね。 この話をするにあたって、サイコロの問題から解説させて下さい。 例えば、「サイコロを2回振る時、出た目の和が5になる確率を求めよ」という問題を解いてみたいと思います。 ご存知の方も多いと思いますが、表を書けば一発解決できます。



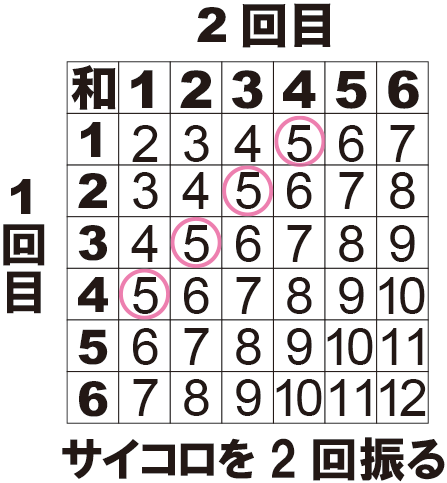
表の左端には1回目にサイコロのどの目が出たか、上端には2回目にサイコロのどの目が出たか、その他のマスは1回目と2回目の合計を表しています。 これで、和が5となるところを選べば良いわけです。 確率は\( \frac{聞かれている事象}{全事象} \)で求まります。5を数えて4つあるので \( \frac{4}{6^2} \)つまり\( \frac{1}{9} \)となる訳です。 まず、Cや Pの違いで悩む前に□の2乗、あるいは3乗となるパターンが基本として存在する事をしっかりおさえて下さい。

順列〜Permutation〜とは?

Pを使う代表例として、1から6のカードが入った袋からカードを元に戻さず2回引く、というような問題があります。 先ほどと同様に和が5になる場合を考えてみましょう。


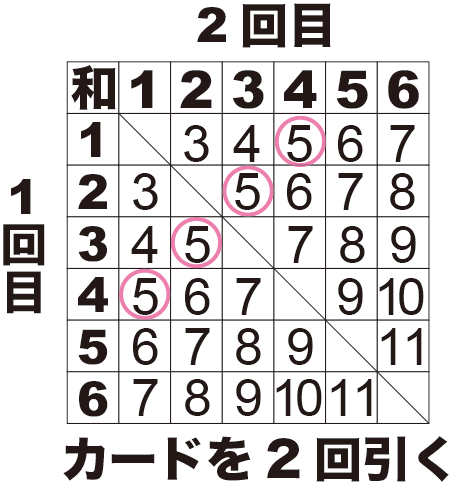
まず、左上から右下に斜線が入っている事を確認して下さい。 これは、カードを元に戻さない、という事なので、2回同じ数字が引けない、という事を意味しています。 全事象はサイコロの場合が\({6^2}\)=36通りだったのに対し、6マスに斜線が入っているので、30通りとなっています。 この問題の答えはどうなるでしょう？表を見ると\( \frac{4}{30} \)となり、約分して\( \frac{2}{15} \)ですよね。 これを表を使わずにやると、そこそこ厄介です。 6枚のカードをボックスに並べていく場合を想像します。

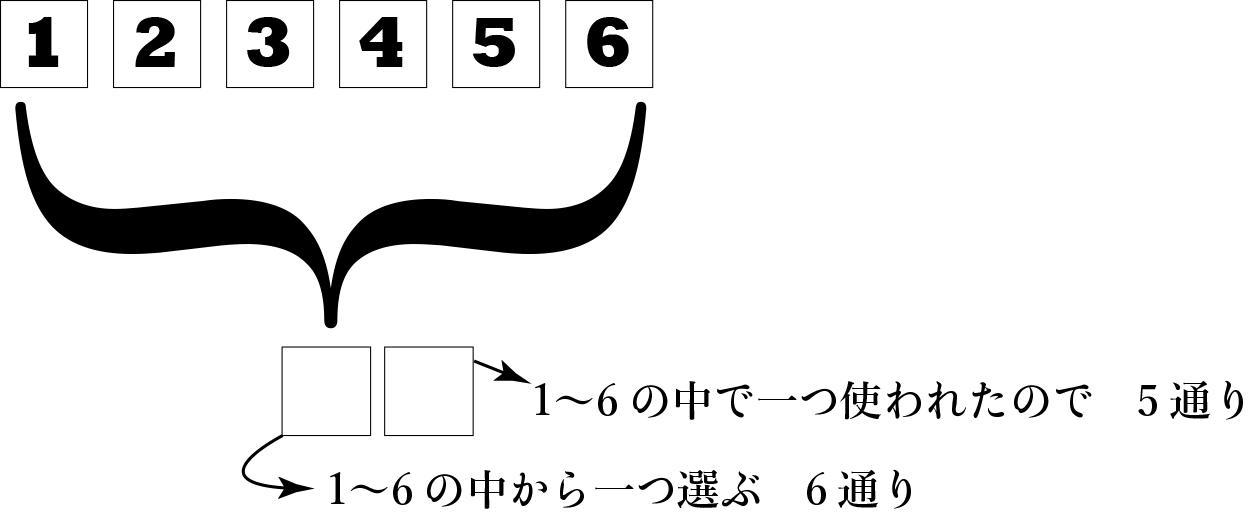
初めのボックスには6通りのカードの入り方がありますが、 2つ目は、もう１つ目のボックスに1つ数字が使われているので、5通りしか入りません。 つまり、6枚のカードから2枚のカードを元に戻さず引く時、その引き方は\( {}_6P_2 = 6×5=30 \)通りあるという事です。 この考え方がPermutation(順列)です。確率を考える際は、これが分母となります。
次に、分子に関して考えます。まず、和が5となるのは(1,4)と(2,3)の２つです。 その上でそれぞれについて\( {}_2P_2 \)ですから、\( {}_2P_2 +{}_2P_2 = 4 \)としなければなりません。 これにより、答えは \( \frac{ {}_2P_2 +{}_2P_2}{_6P_2} = \frac{4}{30} =\frac{2}{15} \)となります。

組み合わせ〜Combination〜とは?
最後に組み合わせです。 「1から6のカードが入った袋からカードを１度に2枚取る」というような問題があります。

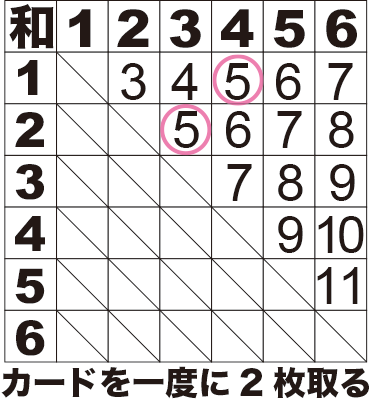
斜線の数が増えましたね。
これは、例えば1,2という順序で取る場合と2,1という順序で取る場合が同一と見做されるために引いた斜線です。
例えば、野球などで巨人vs阪神、という試合と阪神vs巨人という試合は順序が変わっても、 同一と見做す事ができますよね。 この様な場合、\( {}_2C_2 \)と言う表記で6枚の中から2枚を取る(順序は区別しない)事を意味します。 計算でやろうとすると、先ほどの\( {}_6P_2 \)を巨人vs阪神と阪神vs巨人の入れ替えられる通りで割ることになり、 2で割ります。つまり\( {}_6P_2 \)÷2=15となります。 この場合、先ほどと同様に和が5となる場合を求めると、 \( \frac{2}{15} \) となり、Pの時と全く同様の答えが出るのです。 これも表を使わないでやろうとすると、 和が5となるのは(1,4)と(2,3)の２つの組み合わせの中から2つを選ぶ場合となるので、 \( {}_2C_2 \)＋\( {}_2C_2 \)=1+1=2となります。

以上より、「6枚のカードからカードを元に戻さず2枚を引く際、和が5になる確率を求めよ」の答えは\( \frac{2}{15} \)ですが、 PでやってもCでやってもOKという結論が得られました。 和とは交換法則3+2=2+3が成り立つので、先にどちらを引こうとも、結論は変わらない、という事です。 しかし、例えば「初めに引いた数を10の位とし、後から引いた数を1の位とする時、出来上がる数が23を超える確率を求めよ」 などと言われた場合は、当然答えは変わって来ます。 Pでやるのが正解ですよね。

Pでやれば間違えないケースが多いですが、Cでやらないと計算が複雑になるケースが多いです。

そして。一番やってはいけない事を書いて終わりにしたいと思います。 それは、
「全体(分母)は順列で考えたのに、聞かれていること(分子)を求めるためには、組み合わせで考えてしまう事」
です。 こうすると、答えは
\( \frac{ {}_2C_2 +{}_2C_2}{_6P_2} = \frac{2}{30} =\frac{1}{15} \)
となってしまいます。 この様な間違いを避けるために、どの様な考え方で事象を数えたのかを意識しましょう。