私が高校の時、化学を学んでいく中で、ここはまぁ、こういうモンだから。。で流した事が多くありました。 中でも、中和滴定曲線、がその最たるものでした。 「中和点付近では、劇的にpHが変化するので、pH曲線は鉛直になる」 先生がそうおっしゃった時、「なんで劇的に変化するんやねん」と思いました。 大人になって、教える側に回ると、それではいかんな、と思います。 ですので今日は、その理由を考えてみようと思います。


例えば0.1mol/LのHCLが1Lあります。 初めのpHは$\text{pH}=-{\log }_{10}[H^{+}]$ですので、pH=1となります。 これに、0.1mol/LのNaOHを入れていきます。 滴定曲線は$\text{pH}=-{\log }_{10}[H^{+}]$に沿います。NaOHを$x$L入れた時は$0.1x$molの $O{H}^{-}$がある訳ですから、元々0.1molあった$H^{+}$は0.1$x$mol減り、$0.1-0.1x$molとなります。 また、$x$L入れると、溶液の体積は$1+x$ Lとなり、mol濃度は $\frac{0.1-0.1x}{1+x}$mol/Lとなります。 ですので、$\text{pH}=-{\log }_{10}$$\frac{0.1-0.1x}{1+x}$となります。これをグラフにしてみましょう。


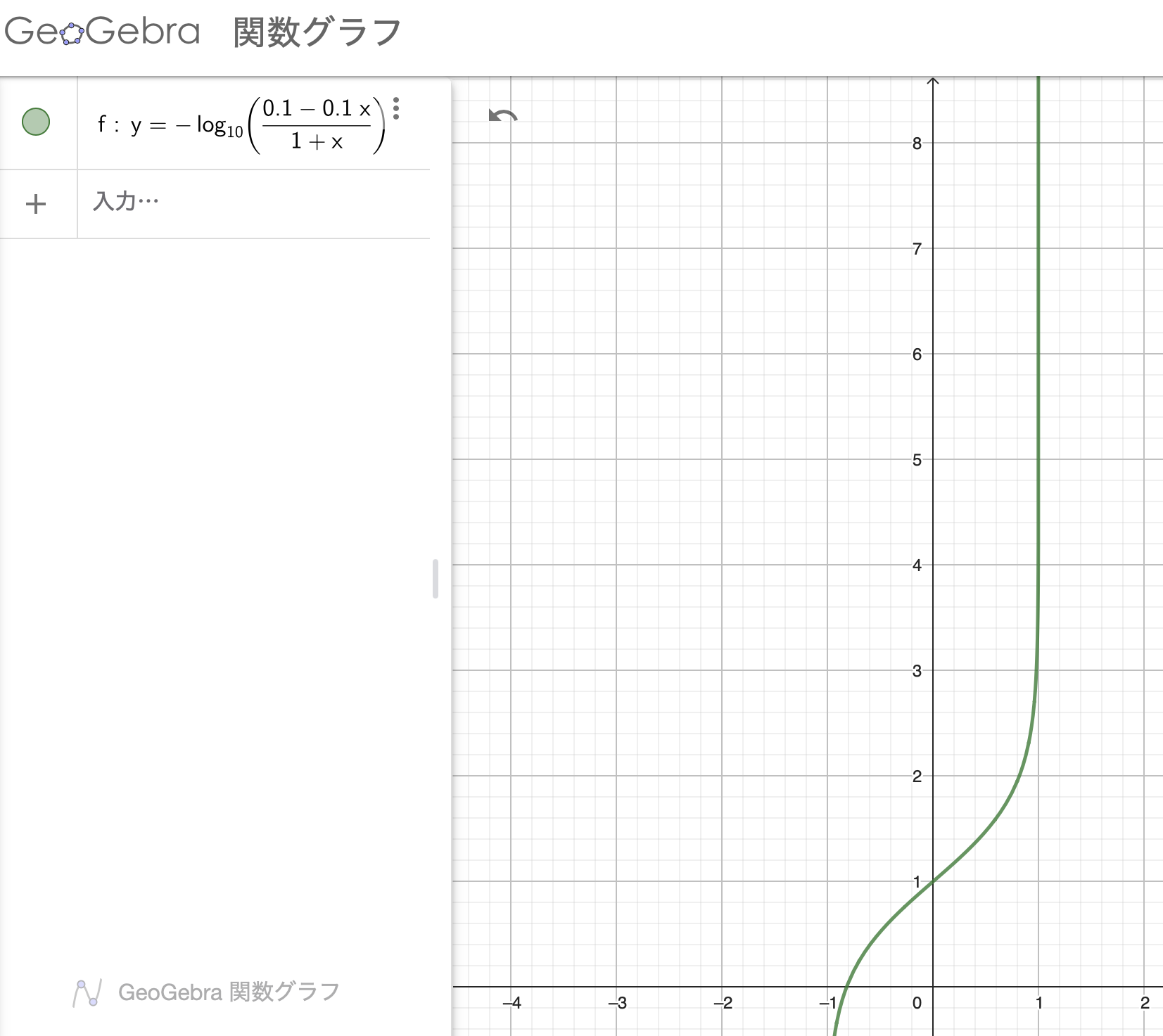
NaOHを1L入れたところで、急激に中和が進む、どころかpHが発散してしまっています。。
pHは14までしか無い訳で、これは現実に反する結果です。 実際は水のイオン積なるものが存在し、摂氏25度で
$[H^{+}][O{H}^{-}]={10}^{-14}$
と決まっており、 これは、水素イオン濃度と水酸化物イオン濃度の積は常に${10}^{-14}$に保たれる、と言うことを意味します。 つまり、HCl由来の$H^{+}$が0になった際、 中和してこれはもう普通の水だから水のイオン積という別ルールが適応され、中性ということだから、 [H+]と[OH-]が同量あり、${10}^{-7}$ずつだよね、つまりpH=7と言う話になるのです。 そしてここからは、水のイオン積のルールに従います。 $[H^{+}][O{H}^{-}]={10}^{-14}$より、$[H^{+}]$ = $\frac{{10}^{-14}}{[O{H}^{-}]}$ですよね。pH=-log10[H+]を変形していきます。 pH=-log10[H+]=-log10(10^-14/[OH-])=14+log10(OH-)となり、話はOHの濃度に転換しました。 ここで、xLのNaOHを滴下した際のOH-は0.1xmolですが、中和で0.1mol減ったため、中和後は0.1x-0.1molとなります。 mol濃度はこれを体積で割りますので、$\frac{0.1x-0.1}{1+x}$mol/Lです。 これを先ほどの式に当てはめて、$\text{pH}=-{\log }_{10}$$\frac{0.1x-0.1}{1+x}$ ですね。これがpH曲線となります。さあ、書いてみましょう。


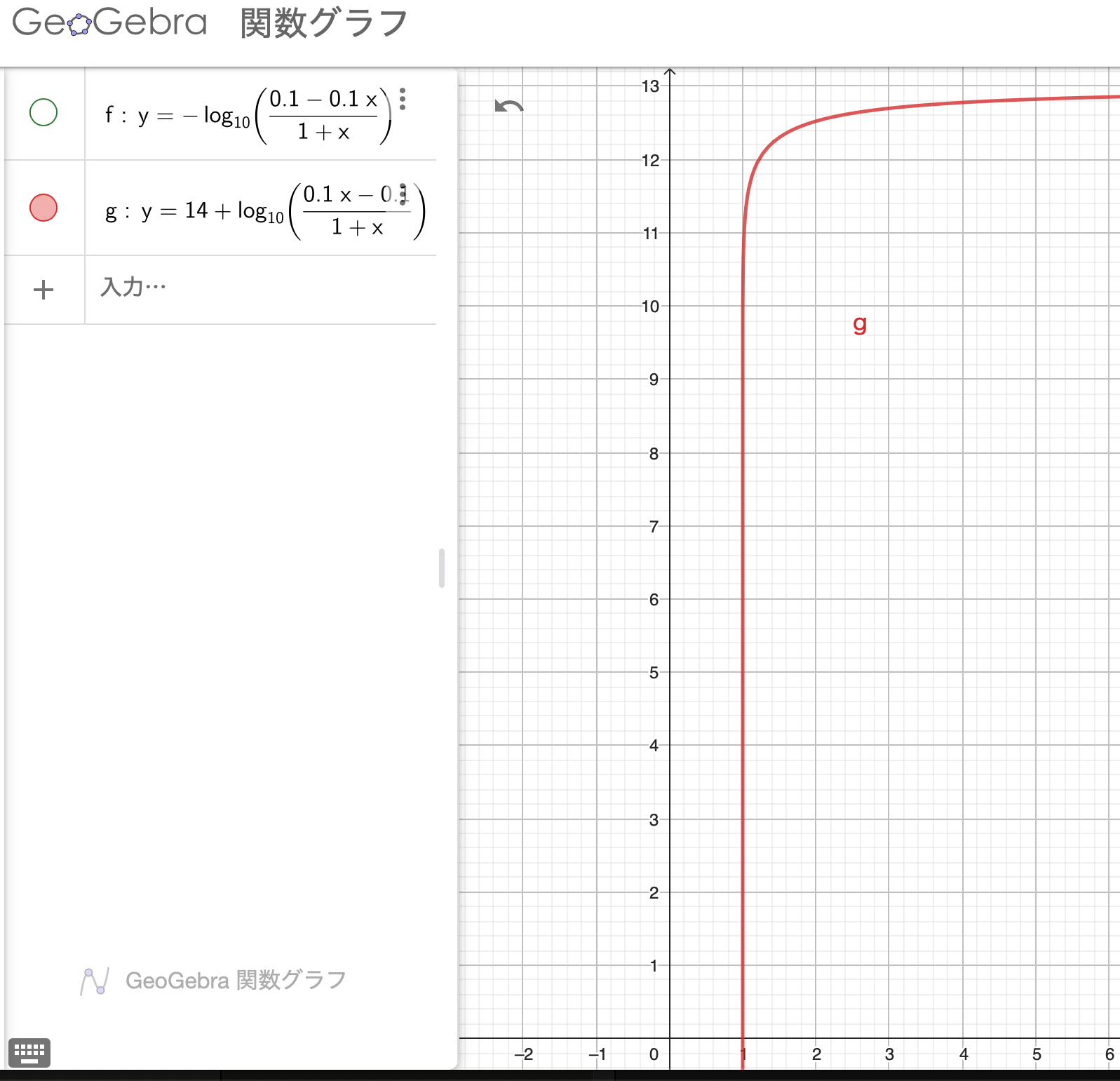
あれ、無限に注いでもpHが13にしかならない感じです。そうです。これは、pH=13のNaOHを注いでいるので当たり前です。 この２本の曲線をpH=7となる点で繋いでみましょう。


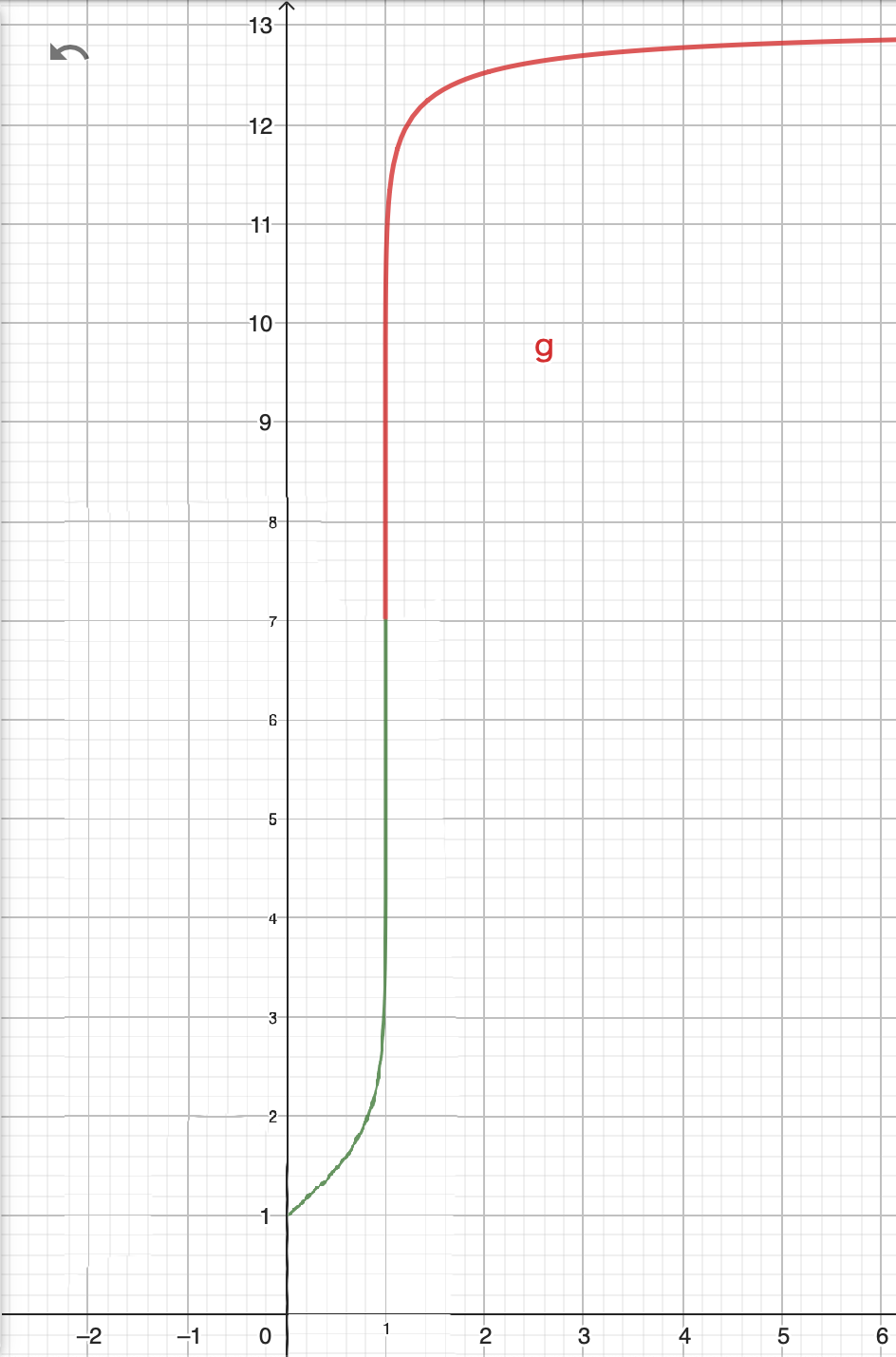
　　いかがでしょうか。見事なpHジャンプを描くことができました。 この様なpHジャンプが起きる理由としては、対数の性質が挙げられます。 $y={\log }_{10}x$のグラフは0付近でマイナス無限大方向に急激に発散していきますが、 この急降下が縦方向に反転された形が2本組み合わさる事で、中和滴定曲線が形造られていたのです。 また、一見すると、中和点について点対称の様に見えますが、本当にそうでしょうか。 反転させて重ねてみると、明らかに点対称にはなりません。


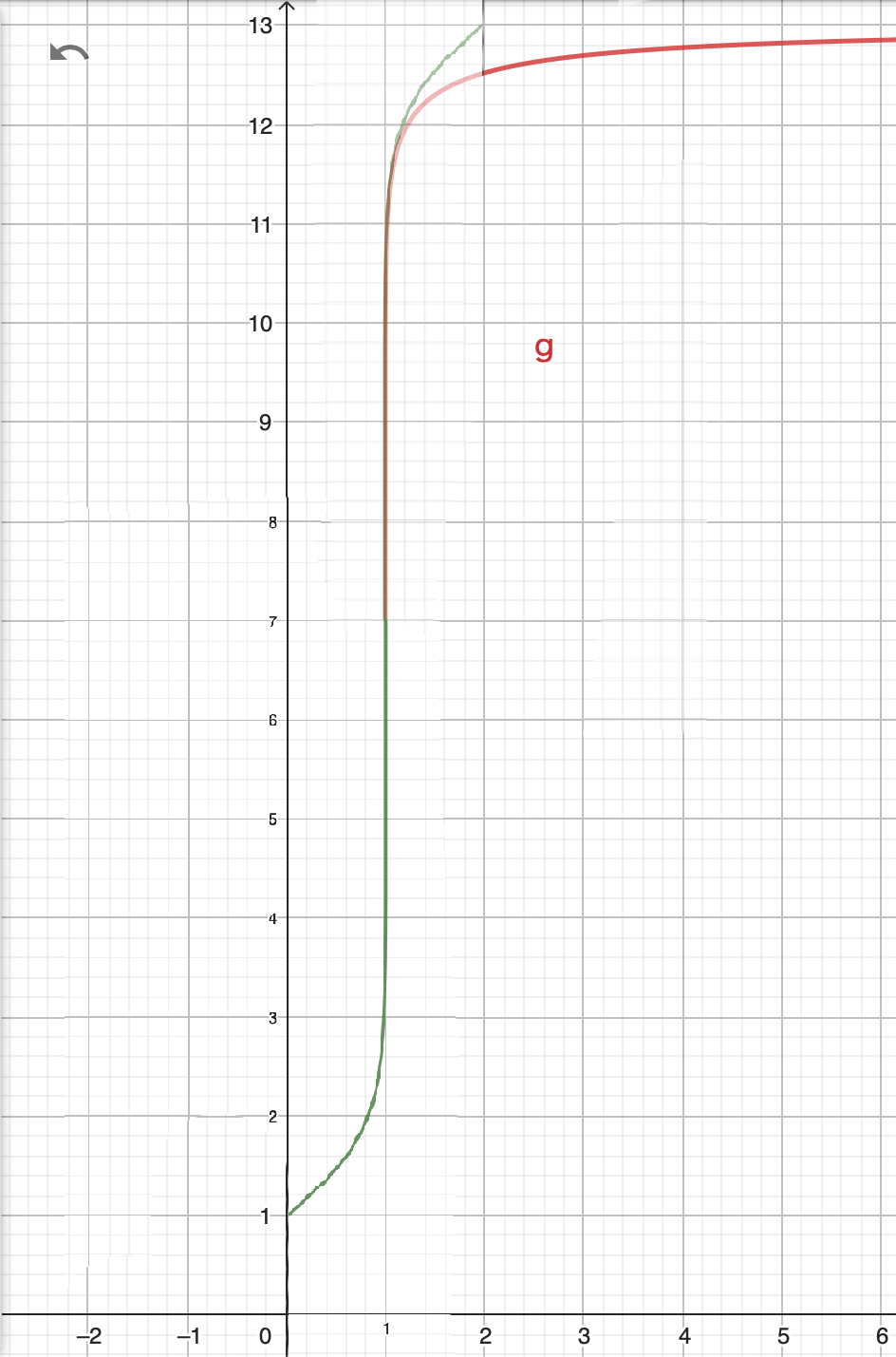
教科書を一歩深掘りすると、深遠な世界が広がっている様です。